Table Of Content

For example, it is possible that measuring participants’ moods before measuring their perceived health could affect their perceived health or that measuring their perceived health before their moods could affect their moods. So the order in which multiple dependent variables are measured becomes an issue. One approach is to measure them in the same order for all participants—usually with the most important one first so that it cannot be affected by measuring the others. Another approach is to counterbalance, or systematically vary, the order in which the dependent variables are measured. It would seem almost wasteful to measure a single dependent variable. Even if you are primarily interested in the relationship between an independent variable and one primary dependent variable, there are usually several more questions that you can answer easily by including multiple dependent variables.
What Are Factorial Experiments and Why Can They Be Helpful?
These measures may be administered using specialized equipment or software. Blinding involves keeping participants, researchers, or both unaware of which treatment group participants are in, in order to reduce the risk of bias in the results. This involves randomly assigning participants to different groups or treatments to ensure that any observed differences between groups are due to the treatment and not to other factors. This design involves dividing participants into blocks based on a specific characteristic, such as age or gender, and then randomly assigning participants within each block to one of two or more treatment groups.
Fractional Factorial Experiments
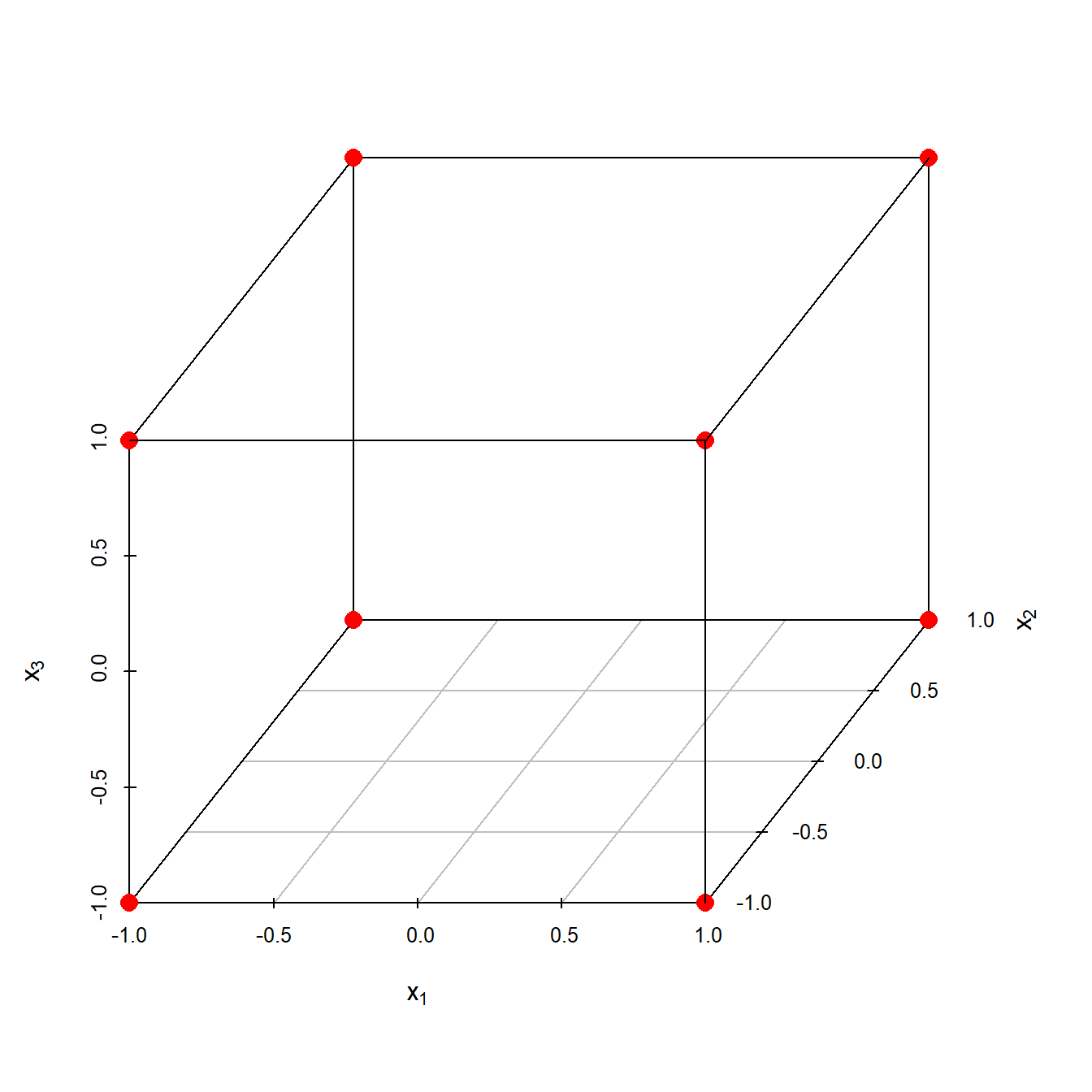
When the number of factors is large (typically more than about 5 factors, but this does vary by application), replication of the design can become operationally difficult. In these cases, it is common to only run a single replicate of the design, and to assume that factor interactions of more than a certain order (say, between three or more factors) are negligible. Under this assumption, estimates of such high order interactions are estimates of an exact zero, thus really an estimate of experimental error. As a further example, the effects of three input variables can be evaluated in eight experimental conditions shown as the corners of a cube. There are many simple examples of two independent variables being dependent on one another to produce an outcome.
Advantages and disadvantages of factorial experiments
This combination of studies is similar in some respects to a factorial experiment but lacks certain unique advantages of factorial studies. The purpose of this commentary is to elaborate on those potential advantages of factorial studies, referring back to the article by Kaplan et al1 for context. The normal probability plot of the effects shows us that two of the factors A and C are both significant and none of the two-way interactions are significant.
A contrast in cell means is a linear combination of cell means in which the coefficients sum to 0. Contrasts are of interest in themselves, and are the building blocks by which main effects and interactions are defined. Treatment combinations are denoted by ordered pairs or, more generally, ordered tuples. The parentheses are often dropped, as shown in the accompanying table.
Imagine, for example, that a researcher conducts an experiment on the effect of daily exercise on stress. The dependent variable, stress, is a construct that can be operationalized in different ways. For this reason, the researcher might have participants complete the paper-and-pencil Perceived Stress Scale and also measure their levels of the stress hormone cortisol. If the researcher finds that the different measures are affected by exercise in the same way, then he or she can be confident in the conclusion that exercise affects the more general construct of stress. Once the factorial effects have been computed, the natural question is whether they are large enough to be of statistical and scientific interest. Thus, if all factorial terms are included in the model, traditional regression-based inferences cannot be made because there is no estimate of residual error.
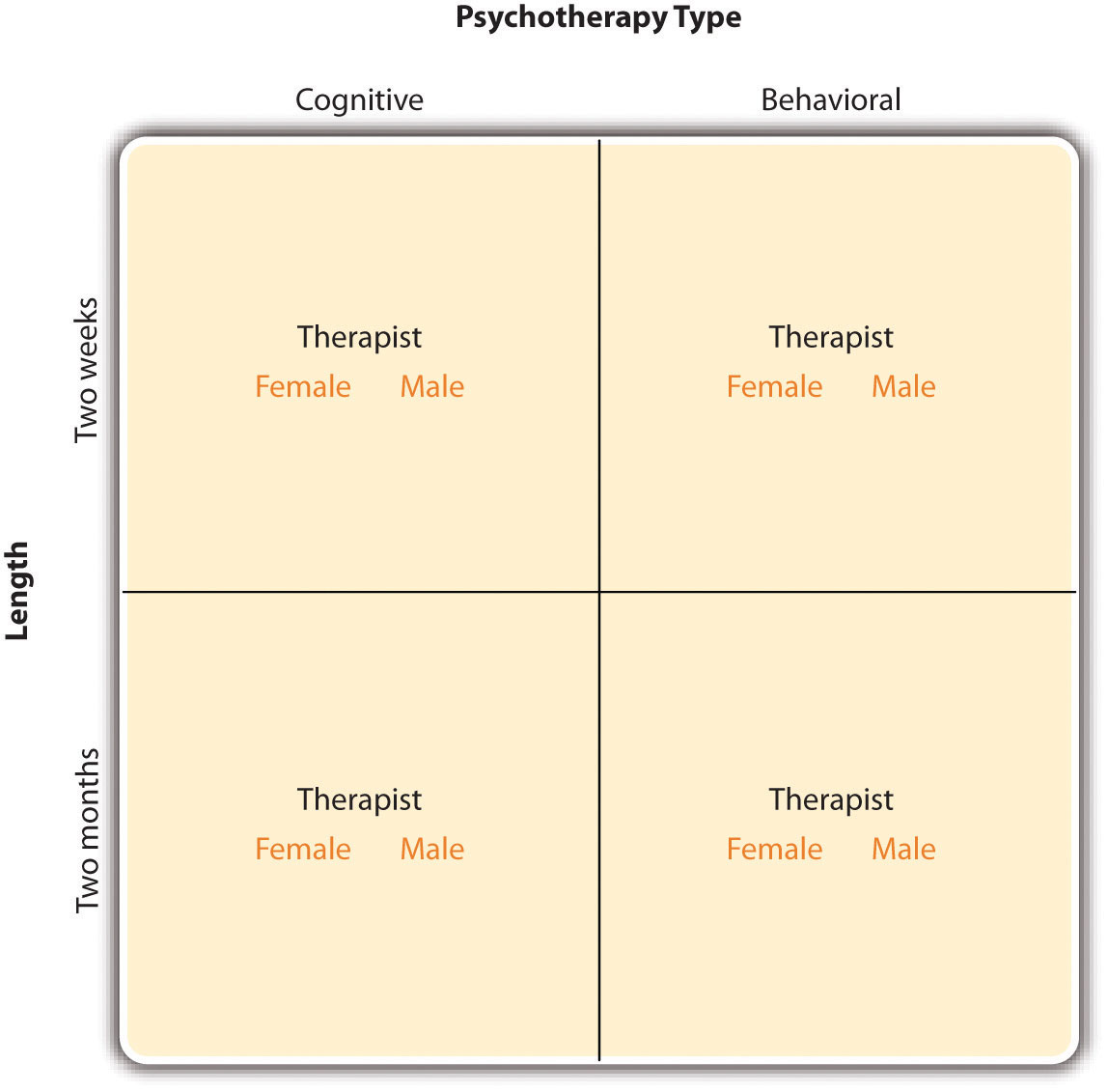
For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone. But they might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions. In the remainder of this section, we will focus on between-subjects factorial designs only. Also, regardless of the design, the actual assignment of participants to conditions is typically done randomly. In many factorial designs, one of the independent variables is a non-manipulated independent variable.
From the example above, a null outcome would exist if you received the same percentage of seizures occurring in patients with varying dose and age. The graphs below illustrate no change in the percentage of seizures for all factors, so you can conclude that the chance of suffering from a seizure is not affected by the dosage of the drug or the age of the patient. Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly. An example graphical representation of a factorial design of experiment is provided in Figure 1 . As with any statistical experiment, the experimental runs in a factorial experiment should be randomized to reduce the impact that bias could have on the experimental results.
In other words, the effect of wearing a shoe does not depend on wearing a hat. More formally, this means that the shoe and hat independent variables do not interact. It would mean that the effect of wearing a shoe on height would depend on wearing a hat. But in some other imaginary universe, it could mean, for example, that wearing a shoe adds 1 to your height when you do not wear a hat, but adds more than 1 inch (or less than 1 inch) when you do wear a hat. This thought experiment will be our entry point into discussing interactions. A take-home message before we begin is that some independent variables (like shoes and hats) do not interact; however, there are many other independent variables that do.
Next, what we did at the end of the process is drop that factor entirely. If a particular factor in the screening experiment turns out to be not important either as a main effect or as part of any interaction we can remove it. This is the second strategy, and for instance in this example we took out factor B completely from the analysis. Even with just one observation per cell, by carefully looking at the results we can come to some understanding as to which factors are important.
Distributive randomization: a pragmatic fractional factorial design to screen or evaluate multiple simultaneous ... - BMC Medical Research Methodology
Distributive randomization: a pragmatic fractional factorial design to screen or evaluate multiple simultaneous ....
Posted: Mon, 11 Mar 2024 07:00:00 GMT [source]
In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In a between-subjects factorial design, all of the independent variables are manipulated between subjects. For example, all participants could be tested either while using a cell phone or while not using a cell phone and either during the day or during the night. This would mean that each participant would be tested in one and only one condition.
This can be conducted with or without replication, depending on its intended purpose and available resources. It will provide the effects of the three independent variables on the dependent variable and possible interactions. Having included all the terms back into a full model we have shown how to produce a normal plot. Remember that all of these effects are 1 degree of freedom contrasts of the original data, each one of these is a linear combination of the original observations, which are normally distributed with constant variance.
Investigators may wish to adjust ICs to enhance their compatibility with other components. For instance, investigators might choose to reduce the burden of an IC by cutting sessions or contact times. This might reduce the meaning of the factor because it might make the IC unnecessarily ineffective or unrepresentative. The factorial design of experiment is described with examples in Video 1. Other terms for "treatment combinations" are often used, such as runs (of an experiment), points (viewing the combinations as vertices of a graph, and cells (arising as intersections of rows and columns).

No comments:
Post a Comment